Stylization Control

We propose a modified formulation to control the strenght of stylization. Below, we compare this formulation to the one used by Li et. al.. Li et. al. use only one parameter \(\gamma\):

\begin{equation*} \hat{I}_l = d_l \left( \gamma \left( C_l^s ( e_l( \hat{I}_{l+1})) \right) + (1-\gamma) e_l (\hat{I}_{l+1} ) \right).\label{eq:theirs} \end{equation*}

\(\gamma\) controls the stylization at each layer. This formulation necessarily loses content information at each layer, since neither the encoders nor the decoders are perfect.

Our formulation has two parameters \(\gamma\) and \(\delta\):

\begin{equation*} \hat{I}_l = d_l \left( \gamma \left( \delta C_l^s( e_l( \hat{I}_{l+1})) + (1-\delta)C_l^s( e_l( {I}^c) ) \right) + (1-\gamma) e_l(I^c) \right), \label{eq:ours} \end{equation*}

Here, \(\delta\) controls the stylization at each layer, while \(\gamma\) trades off original content image features against features that are already stylized by preceding layers, but have accumulated encoding and decoding artifact in the process. The figure below shows how original and stylized/decoded content information flows through the network in the two formulations. Setting \(\gamma=\delta\) yields a simple, effective control of stylization strength though, as also shown below. Obviously, \(\gamma\) and \(\delta\) can be set per layer if desired. For our experiments though, we keep them constant across layers.

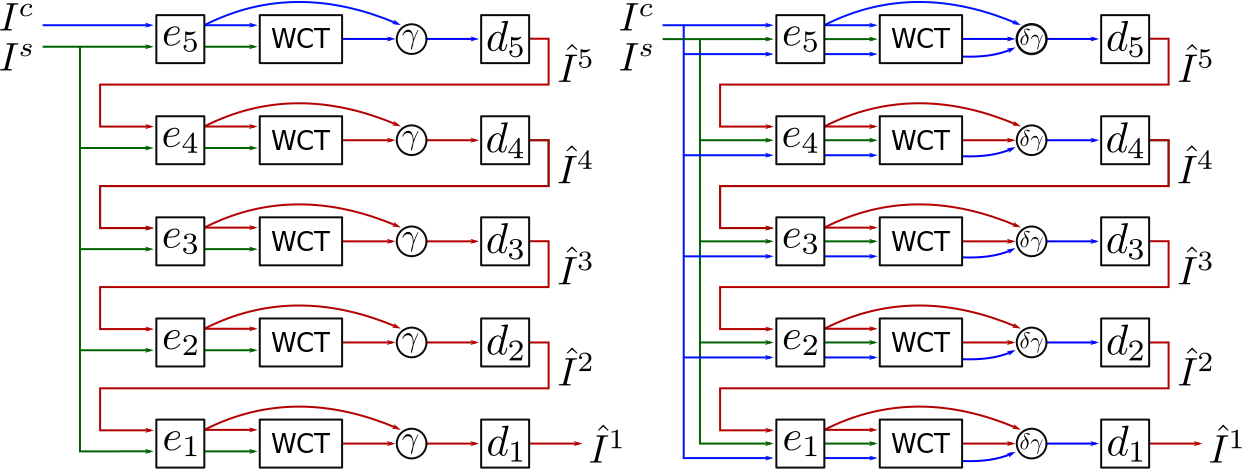
Left: Li et al only use the original content features (in blue) at the very beginning. Even if the modifications to style are set to be minor, the result shows an accumulation of artifacts from successive encoding and decoding steps. Right: we allow the use of original content information at every step of the stylization process. This helps the preservation of detail if desired.